Prior, Posterior, Sample

ch1

In more specific, it is the idea of Methods of Moments. This is the way of matching prior distribution to $\bar{X}$distribution.

Conditional Independence

$$P(F\cap G|H)=P(F|H)P(G|H)$$

Bayes structure

$$p(\theta|y)=\dfrac{p(y|\theta)p(\theta)}{\int_\Theta p(y|\tilde{\theta})p(\tilde{\theta})d\tilde{\theta}}$$

(1) $p(y|\theta)$is the distribution of y conditioned on $\theta$. Like Frequentist, Bayesian assumes a specific form of sampling distribution.

(2) $p(\theta)$is the distribution of $\theta$. From a bayesian point of view, parameter is not constant but random variable.

(3) $p(\theta|y)$reflects how strongly we believe our parameter.

Example

infection

We want to investigate the infection rate($\theta$) in a small city. This rate impacts on the public health policy. Let's say we just sample 20 people.

Parameter and sample space

$$\theta \in \Theta=[0,1] \;\; y=\{0,1,...,20\}$$

Parameter can be on parameter space, from 0 to 1 here. Data y means the number of infected people among 20.

Sampling model

$$Y|\theta \sim binomial(20,\theta)$$

fig1 1

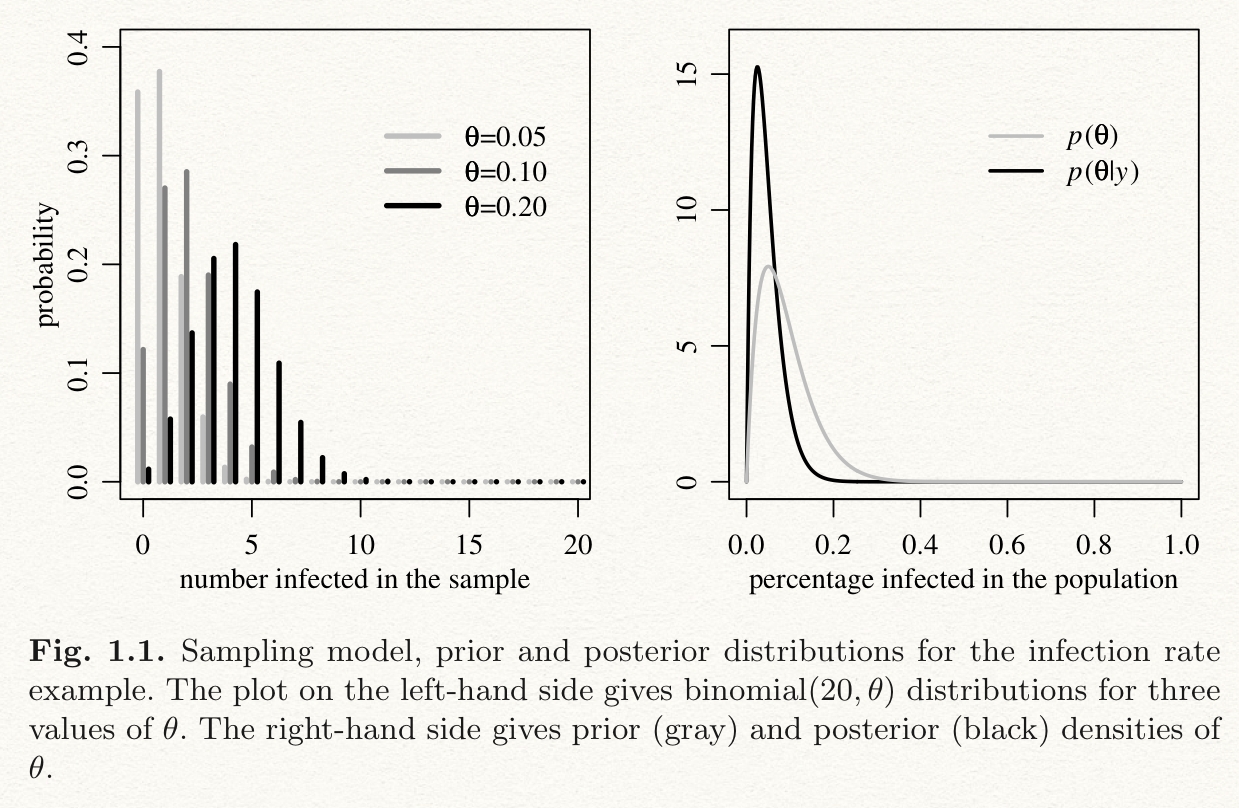
Prior distribution

It is the information about the parameter we know using prior researches. Let's say infection rate has a range (0.05, 0.20) and mean rate is 0.10. In this case, the distribution of parameter would be included in (0.05, 0.20) and expectation should be close to 0.10.

There are a lot of distributions matching this condition, but we just select one distribution convenient in multiplying with sampling distribution(called conjugacy).

$$\theta \sim beta(2,20)$$

$$E[\theta]=0.09 \\ Pr(0.05<\theta<0.20)=0.66$$

The sum of parameters a+b in beta distribution is equal to how much I believe the prior distribution. Because, when this sum becomes increased it shows a strong prior. $Pr(0.05<\theta<0.20)$becomes bigger when the sum gets bigger.

Posterior distribution

We update the parameter information by multiplying Prior distribution with Sampling density.

$$Y|\theta \sim binomial(n,\theta), \theta \sim beta(a,b) \\ \theta|Y \sim beta(a+y, b+n-y)$$

$$\theta|\{Y=0\} \sim beta(2,40)$$

We reflect {Y=0} as we observe this in sample.

Sensitivity analysis

$$E[\theta|Y=y]=\dfrac{a+y}{a+b+n}=\dfrac{n}{a+b+n}\dfrac{y}{n}+\dfrac{a+b}{a+b+n}\dfrac{a}{a+b}=\dfrac{n}{w+n}\bar{y}+\dfrac{w}{w+n}\theta_0$$

• $\theta_0$: prior expectation, $\bar{y}$: sample mean

contour

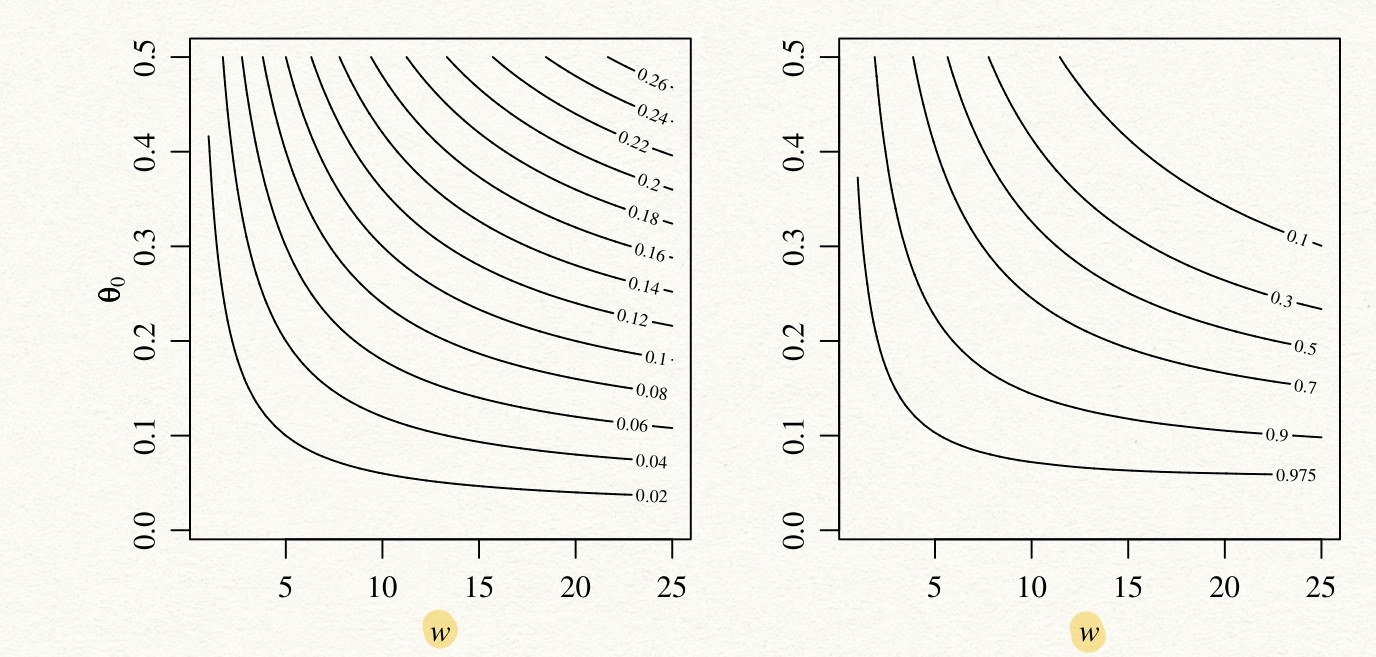
Non-Bayesian methods

$$(\bar{y}-1.96\sqrt{\bar{y}(1-\bar{y})/n}, \bar{y}+1.96\sqrt{\bar{y}(1-\bar{y})/n})$$

$$\hat{\theta} = \dfrac{n}{n+4}\bar{y}+\dfrac{4}{n+4}\dfrac{1}{2}$$

Make a variation.

$$\hat{\theta}=\dfrac{n}{n+\omega}\bar{y}+\dfrac{\omega}{n+\omega}\theta_0$$

Large sample, small sample 2 cases.

Bayesian estimate VS OLS in regression

$$SSR(\beta)=\Sigma^n_{i=1} (y_i-\beta^Tx_i)^2$$

$$SSR(\beta)=\Sigma^n_{i=1} (y_i-x_i^T\beta)^2+\lambda\Sigma^p_{j=1}|\beta_j|^q$$

It is the way of putting log-prior on $\beta$

q

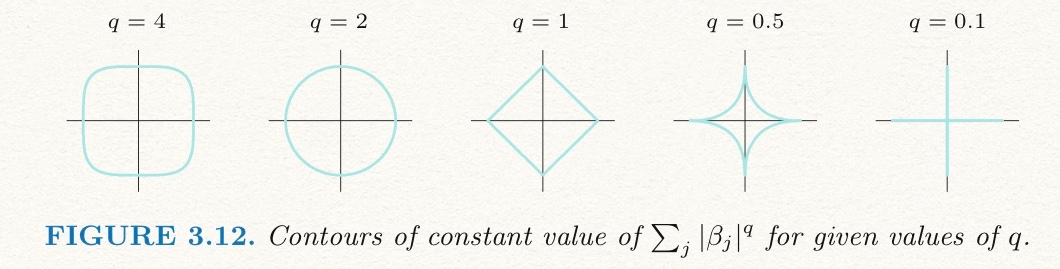
• OLS: Orthogonally project y onto the column space of X

• Bayesian: Doesn't need to be orthogonal between error and $x_i$